Where to Find a Critical Depth Open Channel Flow Spreadsheet
To obtain a critical depth open channel flow spreadsheet for calculating critical depth and/or critical slope for open channel flow, click here to visit our spreadsheet store. Read on for information about the use of a critical depth open channel flow spreadsheet for critical depth and critical slope calculations.
The Froude Number and Critical, Subcritical and Supercritical Flow
Any particular example of open channel flow will be critical, subcritical, or supercritical flow. In general, supercritical flow is characterized by high liquid velocity and shallow flow, while subcritical flow is characterized by low liquid velocity and relatively deep flow. Critical flow is the dividing line flow condition between subcritical and supercritical flow.
The Froude number is a dimensionless number for open channel flow that provides information on whether a given flow is subcritical, supercritical or critical flow. The Froude number is defined to be: Fr = V/(gL)1/2 , where V is the average velocity, g is the acceleration due to gravity, and L is a characteristic length for the particular type of open channel flow. For flow in a rectangular channel: Fr = V/(gy)1/2 , where y is the depth of flow. For flow in an open channel with a shape other than rectangular: Fr = V/[g(A/B)]1/2 , where A is the cross-sectional area of flow, and B is the surface width.
The value of the Froude number for a particular open channel flow situation gives the following information:
- For Fr < 1, the flow is subcritical
- For Fr = 1, the flow is critical
- For Fr > 1, the flow is supercritical
Calculation of Critical Depth
It is sometimes necessary to know the critical depth for a particular open channel flow situation. This type of calculation can be done using the fact that Fr = 1 for critical flow. It is quite straightforward for flow in a rectangular channel and a bit more difficult, but still manageable for flow in a non-rectangular channel.
For flow in a rectangular channel (using subscript c for critical flow conditions), Fr = 1 becomes: Vc/(gyc)1/2 = 1. Substituting Vc = Q/Ac = Q/byc and q = Q/b (where b = the width of the rectangular channel), and solving for yc gives the following equation for critical depth: yc = (q2/g)1/3. Thus, the critical depth can be calculated for a specified flow rate and rectangular channel width.
For flow in a trapezoidal channel, Fr = 1 becomes: Vc/[g(A/B)c]1/2 = 1. Substituting the equation above for Vc together with Ac = yc(b + zyc) and Bc = b + zyc2 leads to the following equation, which can be solved by an iterative process to find the critical depth:
Calculation of Critical Slope
After the critical depth, yc , has been determined, the critical slope, Sc , can be calculate using the Manning equation if the Manning roughness coefficient, n, is known. The Manning equation can be rearranged as follows for this calculation:
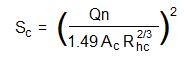 Note that Rhc , the critical hydraulic radius, is given by:
Note that Rhc , the critical hydraulic radius, is given by:
Rhc = Ac/Pc, where Pc = b + 2yc(1 + z2)1/2
Note that calculation of the critical slope is the same for a rectangular channel or a trapezoidal channel, after the critical depth has been determined. The Manning equation is a dimensional equation, in which the following units must be used: Q is in cfs, Ac is in ft2, Rhc is in ft, and Sc and n are dimensionless.
Calculations in S.I. Units
The equations for calculation of critical depth are the same for either U.S. or S.I. units. All of the equations are dimensionally consistent, so it is just necessary to be sure that an internally consistent set of units is used. For calculation of the critical slope, the S.I. version of the Manning equation must be used, giving:
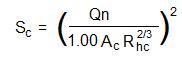 In this equation, the following units must be used: Q is in m3/s, Ac is in m2, Rhc is in m, and Sc and n are dimensionless.
In this equation, the following units must be used: Q is in m3/s, Ac is in m2, Rhc is in m, and Sc and n are dimensionless.
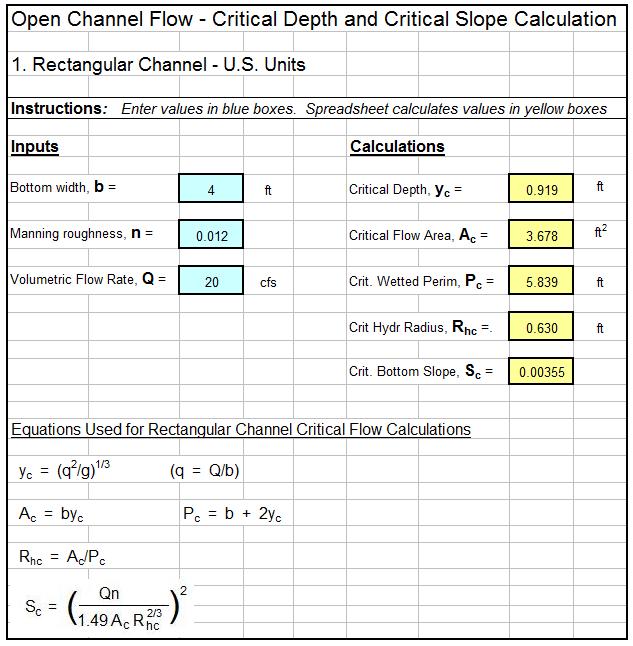
A Critical Depth Open Channel Flow Spreadsheet Screenshot
The critical depth open channel flow spreadsheet template shown below can be used to calculate the critical depth and critical slope for a rectangular channel with specified flow rate, bottom width, and Manning roughness coefficient. Why bother to make these calculations by hand? This Excel spreadsheet and others with similar calculations for a trapezoidal channel are available in either U.S. or S.I. units at a very low cost in our spreadsheet store.
References
1. Munson, B. R., Young, D. F., & Okiishi, T. H., Fundamentals of Fluid Mechanics, 4th Ed., New York: John Wiley and Sons, Inc, 2002.
2. Chow, V. T., Open Channel Hydraulics, New York: McGraw-Hill, 1959.
3. Bengtson, Harlan H. Open Channel Flow II – Hydraulic Jumps and Supercritical and Nonuniform Flow – An online, continuing education course for PDH credit.
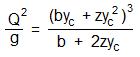
Pingback: Hydraulic Jump Calculations with Excel Spreadsheets | Engineering Excel Spreadsheets
Pingback: How To Calculate Critical Depth | New Tipstoday