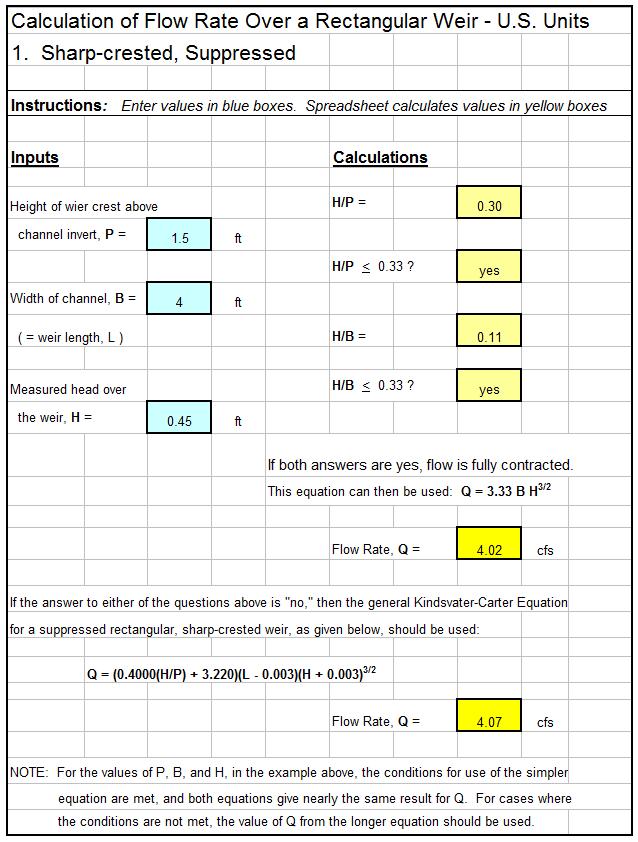
Where to Find a Natural Convection Heat Transfer Coefficient Calculator Spreadsheet
For an Excel spreadsheet to use as a natural convection heat transfer coefficient calculator, click here to visit our spreadsheet store. Why search for heat transfer coefficient correlations or use online calculators, when you can buy a spreadsheet to use as a natural convection heat transfer coefficient calculator for five different configurations for only $14.95. Read on for information about natural convection heat transfer coefficients and Excel spreadsheets to obtain a value for them.
Convection heat transfer takes place between a solid surface and fluid that is at a different temperature and is in contact with the surface. If the fluid is flowing past the surface due to an external driving force like a fan or pump, then the heat transfer is called forced convection. When fluid motion is due to density differences within the fluid (caused by temperature variation), then the heat transfer is called natural convection or free convection.
Newton’s Law of Cooling for Natural Convection Heat Transfer Coefficient Calculator
Newton’s Law of Cooling [ Q = hA(Ts – Tf) ] is a simple expression used for the rate of convective heat transfer with either forced or natural convection. The parameters in Newton’s Law of Cooling are:
- Q, the rate of forced convection heat transfer (Btu/hr – U.S. or W – S.I.)
- Ts, the solid temperature (oF – U.S. or oC – S.I.)
- Tf, the fluid temperature (oF – U.S. or oC – S.I.)
- A, the area of the surface that is in contact with the fluid (ft2 – U.S. or m2 – S.I.)
- h, the convective heat transfer coefficient (Btu/hr-ft2–oF – U.S. or W/m2-K – S.I.)
Dimensionless Nusselt, Rayleigh, Grashof, and Prandtl Numbers
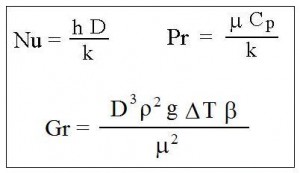 A natural convection heat transfer coefficient calculator typically makes estimations using correlations of dimensionless numbers, specifically correlations of Nusselt number (Nu) with Prandtl number (Pr), Grashof number (Gr), and/or Rayleigh number (Ra), where Ra = GrPr. The Nusselt, Grashof and Prandtl numbers are defined in the box at the left.
A natural convection heat transfer coefficient calculator typically makes estimations using correlations of dimensionless numbers, specifically correlations of Nusselt number (Nu) with Prandtl number (Pr), Grashof number (Gr), and/or Rayleigh number (Ra), where Ra = GrPr. The Nusselt, Grashof and Prandtl numbers are defined in the box at the left.
Following is a list of the parameters that appear in these dimensionless numbers, with units are given for both the U.S engineering system and S.I. system of units:
- D, a characteristic length parameter (e.g. diameter for natural convection from a circular cylinder or a sphere or height of a vertical plate) (ft for U.S., m for S.I.)
- ρ, the density of the fluid (slugs/ft3 for U.S., Kg/m3 for S.I.)
- μ, the viscosity of the fluid (lb-sec/ft2 for U.S., N-s/m2 for S.I.)
- k, the thermal conductivity of the fluid (Btu/hr-ft-oF for U.S., W/m-K for S.I.)
- Cp, the heat capacity of the fluid (Btu/lb-oF for U.S., J/kg-K for S.I.)
- g, the acceleration due to gravity (32.17 ft/sec2 for U.S., 9.81 m/s2 for S.I.)
- β, the coefficient of volume expansion of the fluid ( oR for U.S., K for S.I.)
- ΔT, the temperature difference between the solid surface and the fluid ( oF for U.S., oC or K for S.I.)
The following sections provide equations for estimating the heat transfer coefficient for several common natural convection configurations.
Natural Convection Heat Transfer Calculator for a Vertical Plane
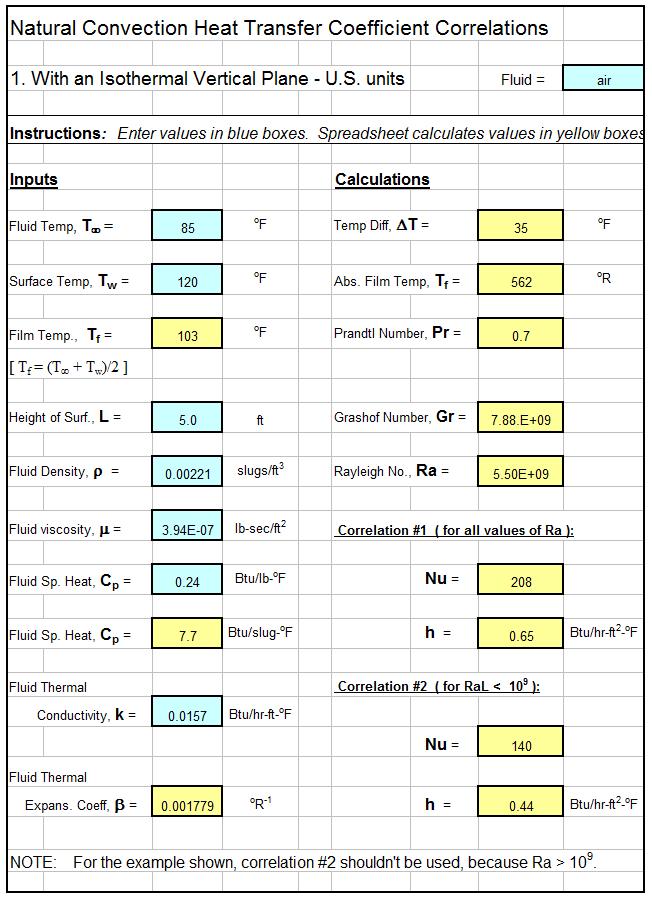
 The box at the right shows two correlations for convection heat transfer between a vertical plane and a fluid of different temperature in contact with it. The first can be used for all values of Rayleigh number and the second is only for laminar flow, indicated by Ra < 109. The screenshot image below shows an example of an Excel spreadsheet to use as a natural convection heat transfer coefficient calculator for a vertical plate using the two equations shown here.
The box at the right shows two correlations for convection heat transfer between a vertical plane and a fluid of different temperature in contact with it. The first can be used for all values of Rayleigh number and the second is only for laminar flow, indicated by Ra < 109. The screenshot image below shows an example of an Excel spreadsheet to use as a natural convection heat transfer coefficient calculator for a vertical plate using the two equations shown here.
An Excel Spreadsheet as a Natural Convection Heat Transfer Calculator
For low cost, easy to use Excel spreadsheet packages to use as a natural convection heat transfer coefficient calculator for natural convection from a vertical plane, a horizontal plane, an inclined plane, a horizontal cylinder or a sphere in either U.S. or S.I. units (for only $16.95), click here to visit our spreadsheet store.
References
1. Incropera, F.P., DeWitt, D.P, Bergman, T.L., & Lavine, A.S., Fundamentals of Heat and Mass Transfer, 6th Ed., Hoboken, NJ, John Wiley & Sons, (2007).
2. Lienhard, J.H, IV and Lienhard, J.H. V, A Heat Transfer Textbook: A Free Electronic Textbook
3. Bengtson, Harlan H, Fundamentals of Heat Transfer, an online continuing education course for engineering PDH credit
4. Bengtson, Harlan H., Convection Heat Transfer Coefficient Estimation, an online continuing education course for PDH credit.