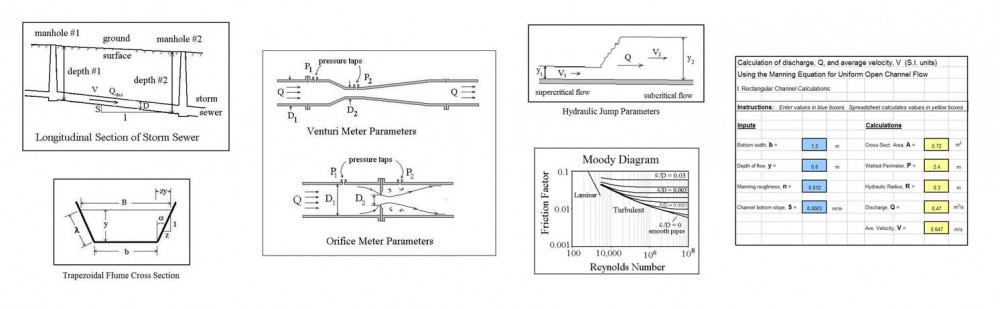
Where to Find a Rectangular Weir Flow Calculator Spreadsheet
For a rectangular weir flow calculator spreadsheet, click here to visit our spreadsheet store. Obtain a convenient, easy to use spreadsheet to use as a rectangular weir flow calculator at a reasonable price. Read on for information about Excel spreadsheets that can be used as contracted rectangular weir open channel flow calculators.
The following section, which gives background on sharp crested rectangular weirs in general, also appears in the companion article, “Suppressed Rectangular Weir Calculations with an Excel Spreadsheet”
Background on Sharp Crested Rectangular Weirs in General
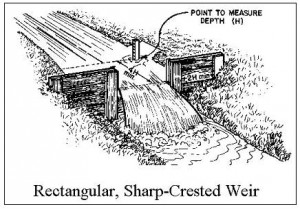 The picture at the left shows a rectangular weir measuring open channel flow rate in a natural channel. The diagram below right shows a longitudinal cross-section of a sharp crested weir, with some of the terminology and parameters often used for sharp crested weirs included on the diagram.
The picture at the left shows a rectangular weir measuring open channel flow rate in a natural channel. The diagram below right shows a longitudinal cross-section of a sharp crested weir, with some of the terminology and parameters often used for sharp crested weirs included on the diagram.
The weir crest is the top of the weir. For a rectangular weir it is the straight, level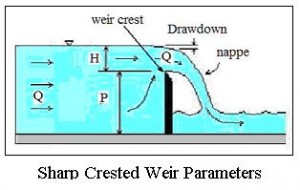 bottom of the rectangular opening through which water flows over the weir. The term nappe is used for the sheet of water flowing over the weir. The equations for calculating flow rate over a weir in this article require free flow, which takes place when there is air under the nappe. The drawdown is shown in the diagram as the decrease in water level going over the weir due to the acceleration of the water. The head over the weir is shown as H in the diagram; the height of the weir crest is shown as P; and the open channel flow rate in the open channel (and over the weir) is shown as Q.
bottom of the rectangular opening through which water flows over the weir. The term nappe is used for the sheet of water flowing over the weir. The equations for calculating flow rate over a weir in this article require free flow, which takes place when there is air under the nappe. The drawdown is shown in the diagram as the decrease in water level going over the weir due to the acceleration of the water. The head over the weir is shown as H in the diagram; the height of the weir crest is shown as P; and the open channel flow rate in the open channel (and over the weir) is shown as Q.
Image Credits: Rectangular, Sharp-Crested Weir: flowmeterdirectory.co.uk
Sharp Crested Weir Parameters: H. H. Bengtson, Ref #2
The Francis Equation for a Rectangular Weir Flow Calculator
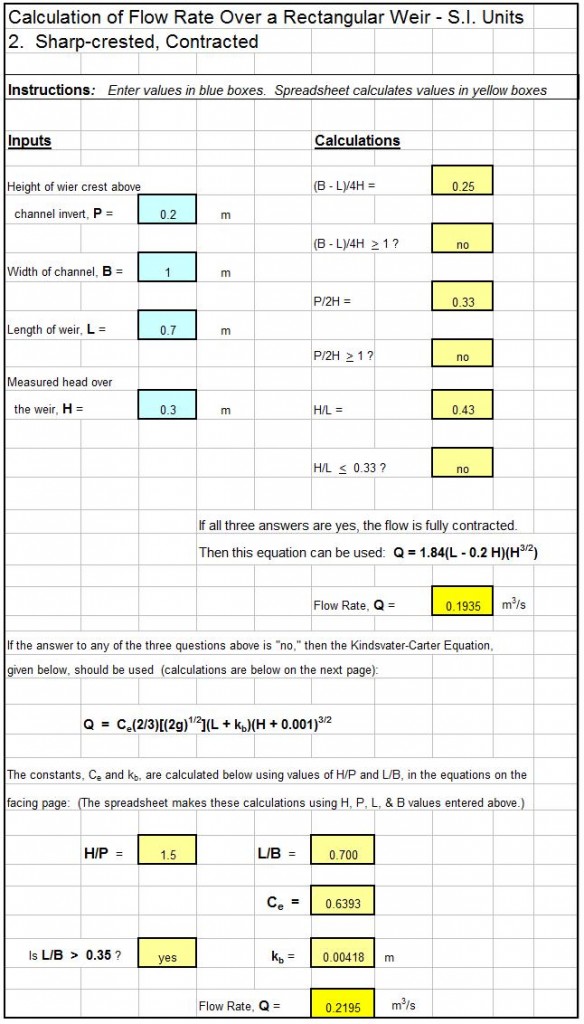
 A contracted rectangular weir is one for which the weir extends across only part of the channel, so that the length of the weir, L, is different from as the width of the channel. The picture at the left shows a contracteded rectangular weir being used to measure the flow of water in a triangular open channel. The diagram below right shows some of the key parameters used in contracted rectangular weir flow rate calculations.
A contracted rectangular weir is one for which the weir extends across only part of the channel, so that the length of the weir, L, is different from as the width of the channel. The picture at the left shows a contracteded rectangular weir being used to measure the flow of water in a triangular open channel. The diagram below right shows some of the key parameters used in contracted rectangular weir flow rate calculations. 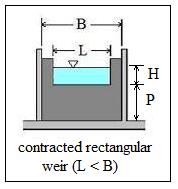 Specifically, the height of the weir crest, P, the head over the weir, H, the weir length, L, and the channel width, B, are shown on the diagram of a contracted rectangular weir in a rectangular channel. The U.S. Bureau of Reclamation, in their Water Measurement Manual (Ref #1 below), recommend the use of the Francis equation (shown below) for completely contracted rectangular weirs, subject to the condition that H/L < 0.33, B – L > 4 Hmax, and P > 2Hmax.
Specifically, the height of the weir crest, P, the head over the weir, H, the weir length, L, and the channel width, B, are shown on the diagram of a contracted rectangular weir in a rectangular channel. The U.S. Bureau of Reclamation, in their Water Measurement Manual (Ref #1 below), recommend the use of the Francis equation (shown below) for completely contracted rectangular weirs, subject to the condition that H/L < 0.33, B – L > 4 Hmax, and P > 2Hmax.
For U.S. units: Q = 3.33(L – 0.2H)H3/2, where
- Q is the water flow rate in ft3/sec,
- L is the length of the weir in ft,
- H is the head over the weir in ft,
- B is the width of the channel in ft, and
- Hmax is the maximum expected head over the weir in ft.
For S.I. units: Q = 1.84(L – 0.2H)H3/2, where
- Q is the water flow rate in m3/sec,
- L is the length of the weir in m, and
- H is the head over the weir in m.
- B is the width of the channel in m, and
- Hmax is the maximum expected head over the weir in m.
Image Credits: Contracted Rectangular Weir picture: Food and Agricultural Organization of the United Nations.
Contracted Rectangular Weir Diagram – Bengtson, Harlan H.
The Kindsvater-Carter Formula for a Rectangular Weir Flow Calculator
If any of the three required conditions given in the previous section are not met, then the more general Kindsvater- Carter Equation, shown below should be used.
U.S. units: Q = Ce(2/3)[(2g)1/2](L + kb)(H + 0.003)3/2
S.I. units: Q = Ce(2/3)[(2g)1/2](L + kb)(H + 0.001)3/2
Ce is a function of L/B and H/P, while kb is a function of L/B. There are graphs, tables and equations available for obtaining values for Ce and kb for specified values of L/B and H/P. The equations given below were prepared from information in Reference #3 at the end of the article.
Ce is dimensionless, so the equation for Ce is as a function of L/B and H/P is the same for both S.I. and U.S. units and is as follows:
Ce = α(H/P) + β, where β = 0.58382 + 0.016218(L/B), and
α = [-0.0015931 + 0.010283(L/B)]/[1 – 1.76542(L/B) + 0.870017(L/B)2]
The equation for kb as a function of L/B has different constants for S.I. and U.S. units. The two versions of the equation for kb are as follows:
U.S. units: for 0 < L/B < 0.35: kb = 0.007539 + 0.001575(L/B) – (kb is in ft)
for 0.35 < L/B < 1.0: kb = -0.34806(L/B)4 + 0.63057(L/B)3 – 0.37457(L/B)2 + 0.09246(L/B) – 0.000197 – (kb is in ft)
S.I. units: for 0 < L/B < 0.35: kb = 0.002298 + 0.00048(L/B) – (kb is in m)
for 0.35 < L/B < 1.0: kb = -0.10609(L/B)4 + 0.1922(L/B)3 – 0.11417(L/B)2 + 0.028182(L/B) – 0.00006 – (kb is in m)
Note that if H/L < 0.33, B – L > 4 Hmax, and P > 2Hmax, then the Francis Equation and the Kindsvater-Carter Equation will give nearly the same value for Q. As conditions diverge more and more from the requirements, the calculations from the two equations will diverge more and more. In these cases the value calculated by the Kindsvater-Carter formula should be used.
An Excel Spreadsheet as a Contracted Rectangular Weir Flow Calculator
The Excel spreadsheet template shown below can be used as a contracted rectangular weir flow calculator, using both the Francis equation and the Kindsvater-Carter equation. Only four input values are needed. They are the height of the weir crest above the channel invert, P; the width of the channel, B; the weir length L; and the measured head over the weir, H. With these four input values, the Excel formulas will calculate the parameters needed and check on whether the conditions required for use of the Francis equation are met. If the conditions are all met, then the value of Q calculated with the Francis equation can be used. If any of the conditions aren’t met, then the value of Q calculated with the Kindsvater-Carter formula should be chosen. This Excel spreadsheet and others for suppressed and contracted rectangular weir calculations are available in either U.S. or S.I. units at a very low cost in our spreadsheet store.
References
1. U.S. Dept. of the Interior, Bureau of Reclamation, 2001 revised, 1997, 3rd ed, Water Measurement Manual
2. Bengtson, H.H., Sharp Crested Weirs for Open Channel Flow Measurement, an Amazon Kindle ebook.
3. Bengtson, H.H., Open Channel Flow Measurement – Weirs and Flumes, An online continuing education course for PDH credit for Professional Engineers
4. Bengtson, H. H., Sharp-Crested Weirs for Open Channel Flow Measurement, An online continuing education course for PDH credit for Professional Engineers.
5. Merkley, Gary P., Weirs for Flow Measurement Open Course Ware, Utah State University.