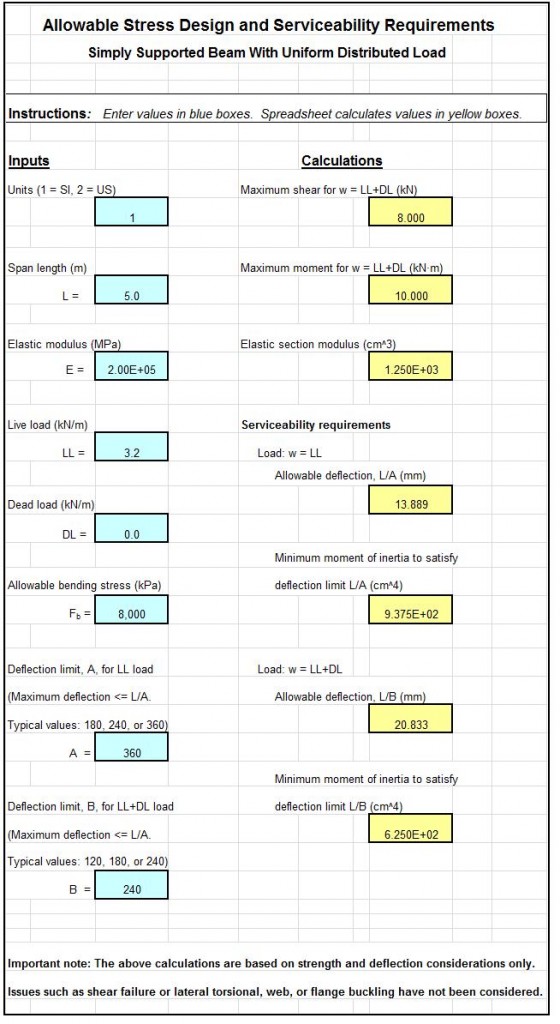
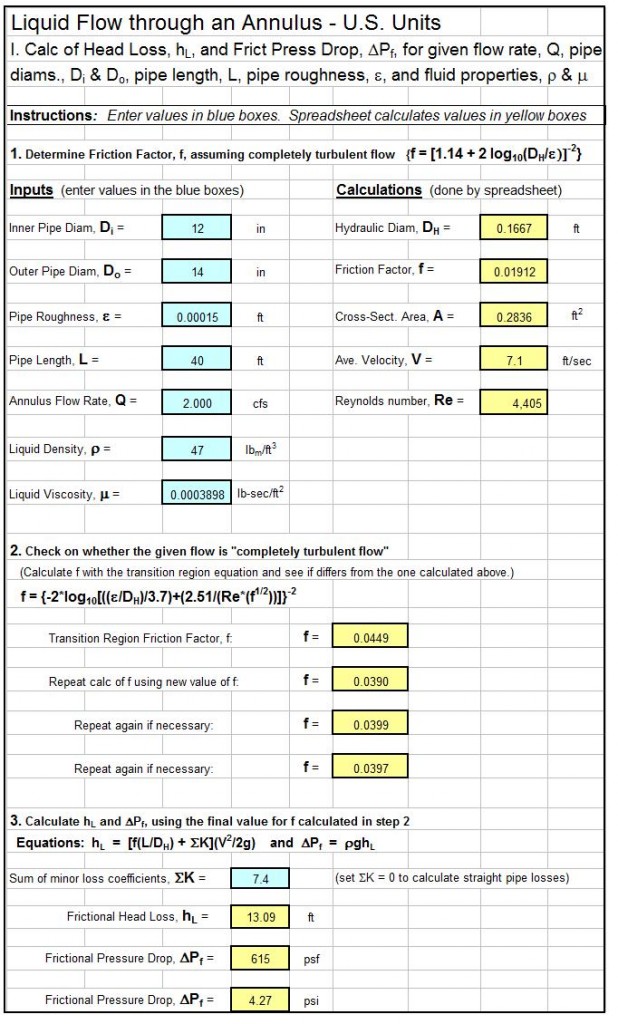
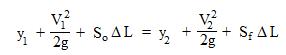Where to Find a Manning Equation Open Channel Flow Calculator Spreadsheet
To obtain a Manning equation open channel flow calculator excel spreadsheet, click here to visit our spreadsheet store. Why use online calculators or make open channel flow/Manning Equation calculations by hand when you can buy a variety of Manning equation open channel flow calculator excel spreadsheets or spreadsheet packages for prices ranging from $6.95 to $27.95? Read on for information about Excel spreadsheets that can be used as a Manning equation open channel flow calculator.
 An excel spreadsheet can conveniently be used as a Manning equation open channel flow calculator. The Manning equation can be used for water flow rate calculations in either natural or man made open channels. Uniform open channel flow calculations with the Manning equation use the channel slope, hydraulic radius, flow depth, flow rate, and Manning roughness coefficient. Image Credit: geograph.org.uk
An excel spreadsheet can conveniently be used as a Manning equation open channel flow calculator. The Manning equation can be used for water flow rate calculations in either natural or man made open channels. Uniform open channel flow calculations with the Manning equation use the channel slope, hydraulic radius, flow depth, flow rate, and Manning roughness coefficient. Image Credit: geograph.org.uk
Uniform Flow for a Manning Equation Open Channel Flow Excel Spreadsheet
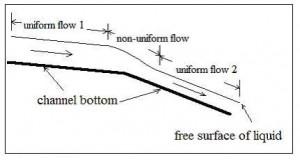
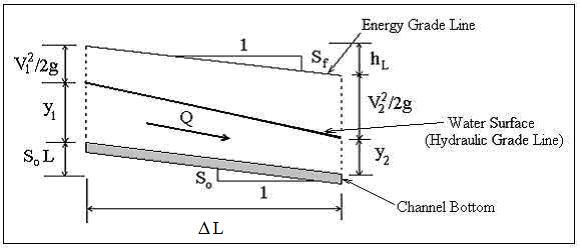
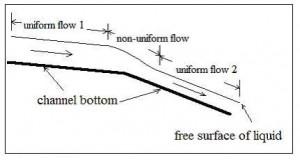 Open channel flow may be either uniform flow or nonuniform flow, as illustrated in the diagram at the left. For uniform flow in an open channel, there is always a constant volumetric flow of liquid through a reach of channel with a constant bottom slope, surface roughness, and hydraulic radius (that is constant channel size and shape). For the constant channel conditions described, the water will flow at a constant depth (usually called the normal depth) for the particular volumetric flow rate and channel conditions. The diagram above shows a stretch of uniform open channel flow, followed by a change in bottom slope that causes non-uniform flow, followed by another reach of uniform open channel flow. The Manning Equation, which will be discussed in the next section, can be used only for uniform open channel flow.
Open channel flow may be either uniform flow or nonuniform flow, as illustrated in the diagram at the left. For uniform flow in an open channel, there is always a constant volumetric flow of liquid through a reach of channel with a constant bottom slope, surface roughness, and hydraulic radius (that is constant channel size and shape). For the constant channel conditions described, the water will flow at a constant depth (usually called the normal depth) for the particular volumetric flow rate and channel conditions. The diagram above shows a stretch of uniform open channel flow, followed by a change in bottom slope that causes non-uniform flow, followed by another reach of uniform open channel flow. The Manning Equation, which will be discussed in the next section, can be used only for uniform open channel flow.
Equation and Parameters for a Manning Equation Open Channel Flow Calculator Excel Spreadsheet
The Manning Equation is:
Q = (1.49/n)A(R2/3)(S1/2) for the U.S. units shown below, and it is:
Q = (1.0/n)A(R2/3)(S1/2) for the S.I. units shown below.
- Q is the volumetric water flow rate in the reach of channel (ft3/sec for U.S.) (m3/s for S.I.)
- A is the cross-sectional area of flow (ft2for U.S.) (m2for S.I.)
- P is the wetted perimeter of the flow (ft for U.S.) (m for S.I.)
- R is the hydraulic radius, which equalsA/P(ft for U.S.) (m for S.I.)
- S is the bottom slope of the channel, (dimensionless or ft/ft -U.S. & m/m – S.I.)
- n is the empirical Manning roughness coefficient, which is dimensionless
The equation V = Q/A, a definition for average flow velocity, can be used to express the Manning Equation in terms of average flow velocity,V, instead of flow rate,Q, as follows:
V = (1.49/n)(R2/3)(S1/2) for U.S. units with V expressed in ft/sec.
Or V = (1.0/n)(R2/3)(S1/2) for S.I. units with V expressed in m/s.
It should be noted that the Manning Equation is an empirical equation. The U.S. units must be just as shown above for use in the equation with the constant 1.49 and the S.I. units must be just as shown above for use in the equation with the constant 1.0.
The Manning Roughness Coefficient for a Manning Equation Open Channel Flow Calculator Excel Spreadsheet
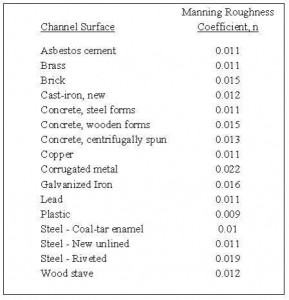 All calculations with the Manning equation (except for experimental determination of n) require a value for the Manning roughness coefficient, n, for the channel surface. This coefficient, n, is an experimentally determined constant that depends upon the nature of the channel and its surface. Smoother surfaces have generally lower Manning roughness coefficient values and rougher surfaces have higher values. Many handbooks, textbooks and online sources have tables that give values of n for different natural and man made channel types and surfaces. The table at the right gives values of the Manning roughness coefficient for several common open channel flow surfaces for use in a Manning equation open channel flow calculator excel spreadsheet.
All calculations with the Manning equation (except for experimental determination of n) require a value for the Manning roughness coefficient, n, for the channel surface. This coefficient, n, is an experimentally determined constant that depends upon the nature of the channel and its surface. Smoother surfaces have generally lower Manning roughness coefficient values and rougher surfaces have higher values. Many handbooks, textbooks and online sources have tables that give values of n for different natural and man made channel types and surfaces. The table at the right gives values of the Manning roughness coefficient for several common open channel flow surfaces for use in a Manning equation open channel flow calculator excel spreadsheet.
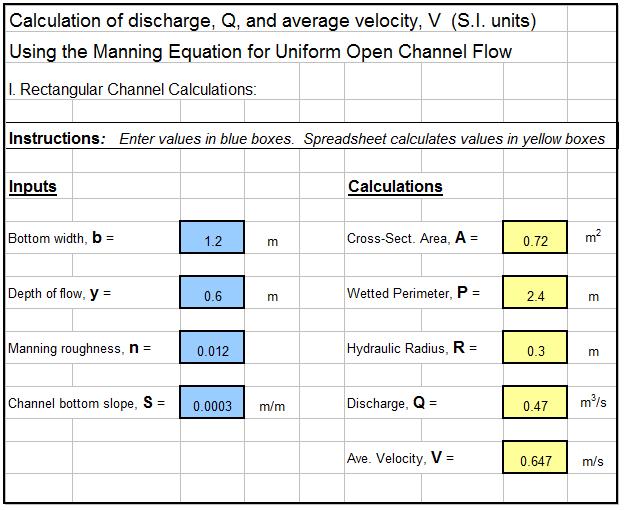
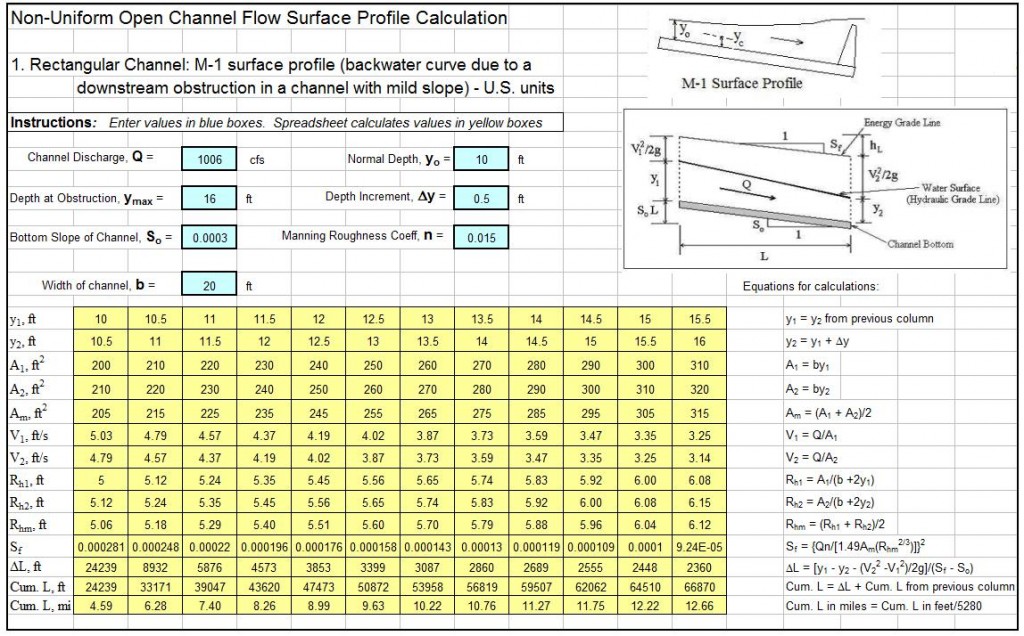
Example Manning Equation Open Channel Flow Excel Spreadsheet
The Manning equation open channel flow calculator excel spreadsheet shown in the image below can be used to calculate flow rate and average velocity in a rectangular open channel with specified channel width, bottom slope, & Manning roughness, along with the flow rate through the channel. This Excel spreadsheet and others for Manning equation open channel flow calculations for rectangular, trapezoidal or triangular channels, in either U.S. or S.I. units are available for very reasonable prices in our spreadsheet store.
References
1. Bengtson, Harlan H., Open Channel Flow I – The Manning Equation and Uniform Flow, an online, continuing education course for PDH credit.
2. U.S. Dept. of the Interior, Bureau of Reclamation, 2001 revised, 1997 third edition, Water Measurement Manual.
3. Chow, V. T., Open Channel Hydraulics, New York: McGraw-Hill, 1959.
4. Bengtson, Harlan H., “Manning Equation Open Channel Flow Excel Spreadsheets,” an online blog article, 2012.
5. Bengtson, Harlan H., “The Manning Equation for Open Channel Flow Calculations“, available as an Amazon Kindle e-book and as a paperback.