Category Archives: Heat Exchanger Design and Heat Transfer Coefficients

Heat Exchanger Thermal Design Calculations Spreadsheet

Posted on by
Reply

Where to Find a Heat Exchanger Thermal Design Calculations Spreadsheet

For a double pipe heat exchanger thermal design calculations spreadsheet, click here to visit our spreadsheet store.  Read on for information about the use of a heat exchanger design thermal design calculations spreadsheet for a double pipe heat exchanger.

The Basic Equation for a Heat Exchanger Thermal Design Calculations Spreadsheet

The basic heat exchanger design equation is:  Q = U A ΔTlm,    where:

  • Q = the rate of heat transfer between the two fluids in the heat exchanger in But/hr (kJ/hr for S.I. units)
  • U is the overall heat transfer coefficient in Btu/hr-ft2–oF  (kJ/hr-m2-K for S.I. units)
  • A is the heat transfer surface area in ft2 (m2 for S.I. units)
  • ΔTlm is the log mean temperature difference in oF,  (K for S.I units)  calculated from the inlet and outlet temperatures of both fluids.

For a heat exchanger thermal design calculations spreadsheet, the heat exchanger equation can be used to calculate the required heat exchanger area for known or estimated values of the other three parameters, Q, U, and ΔTlm.  Each of those parameters will be discussed briefly in the next three sections.

The Log Mean Temperature Difference, ΔTlm , for a Heat Exchanger Design Spreadsheet

Equation for heat exchanger thermal design calculations spreadsheetThe driving force for a heat transfer process is always a temperature difference. For heat exchangers, there are always two fluids involved, and the temperatures of both are changing as they pass through the heat exchanger.  Thus some type of average temperature difference is needed.  Many heat transfer textbooks (e.g. 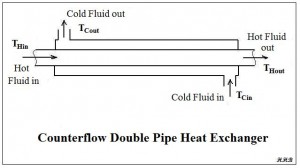ref #1 below) show double pipe heat exchanger diagram for heat exchanger thermal design calculations spreadsheetthat the log mean temperature difference is the appropriate average temperature difference to use for heat exchanger design calculations.  The definition of the log mean temperature difference is shown in the figure above.  The meanings of the four temperatures in the log mean temperature difference equation are rather self explanatory as shown in the diagram of a counterflow double pipe heat exchanger at the right.

The Heat Transfer Rate, Q, for a Heat Exchanger Thermal Design Calculations Spreadsheet

In order to use the heat exchanger design equation to calculate a required heat transfer area,  a value is needed for the heat transfer rate, Q.  This rate of heat flow can be calculated if the flow rate of one of the fluids is known along with its specific heat and the required temperature change for that fluid. The equation to be used is shown below for both the hot fluid and the cold fluid:

Q = mH CpH (THin – THout) = mC CpC (TCout – TCin), where

  • mH is the mass flow rate of the hot fluid in slugs/hr (kg/hr for S.I. units).
  • CpH is the specific heat of the hot fluid in Btu/slug-oF (kJ/kg-K for S.I. units).
  • mC is the mass flow rate of cold fluid in slugs/hr (kg/hr for S.I. units).
  • CpC is the specific heat of the cold fluid in Btu/slug-oF (kJ/kg-K for S.I. units).
  • The temperatures (THin, THout, TCout, & TCin) are the hot and cold fluid temperatures going in and out of the heat exchanger, as shown in the diagram above.  They should be in oF for U.S. or K for S.I. units.

The heat transfer rate, Q, can be calculated in a preliminary heat exchanger design spreadsheet if the flow rate, heat capacity and temperature change are known for either the hot fluid or the cold fluid. Then one unknown parameter can be calculated for the other fluid.  (e.g. the flow rate, the inlet temperature, or the outlet temperature.)

The Overall Heat Transfer Coefficient, U, for a Heat Exchanger Design Spreadsheet

The overall heat transfer coefficient, U, depends on the convection coefficient inside the pipe or tube, the convection coefficient on the outside of the pipe or tube, and the thermal conductivity of the pipe wall.  See the article, Forced Convection Heat Transfer Coefficient Calculations, for information about calculating the heat transfer coefficients and click here to visit our spreadsheet store, for spreadsheets to calculate the inside and outside convection coefficients and to calculate the overall heat transfer coefficient.

A Heat Exchanger Thermal Design Calculations Spreadsheet

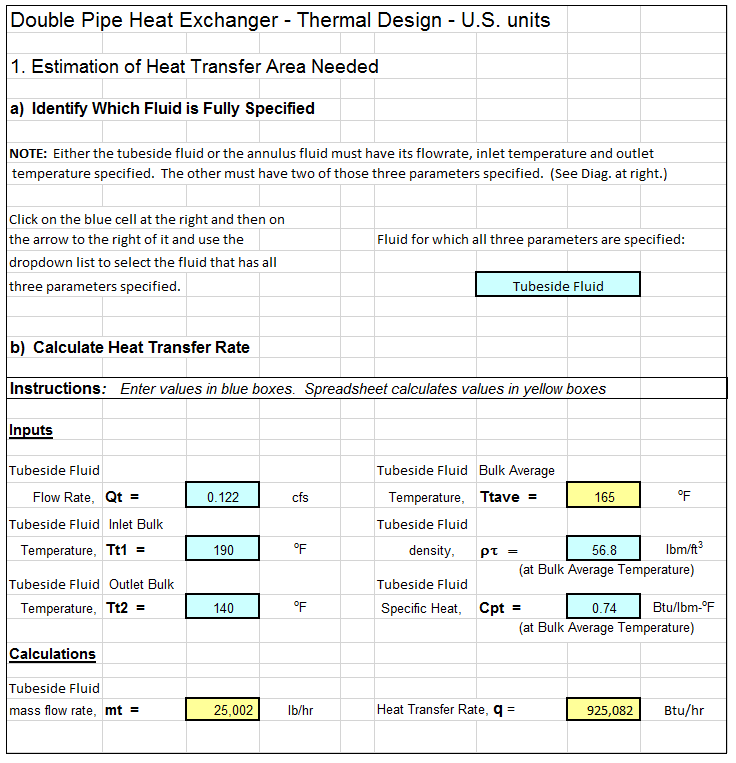
The screenshot below shows a heat exchanger thermal design calculations spreadsheet that can be used to carry out thermal design of a double pipe heat exchanger.  The image shows only the beginning of the calculations.  The rest of the spreadsheet will calculate the length of pipe needed, the length of each pass for a selected number of 180 degree bends, and the pressure drop through the inside of the pipe.  Why bother to make these calculations by hand?  This Excel spreadsheet is available in either U.S. or S.I. units at a very low cost at in our spreadsheet store.

Heat Exchanger Thermal Design Calculations Spreadsheet

References

1. Kuppan, T., Heat Exchanger Design Handbook, CRC Press, 2000.

2. Kakac, S. and Liu, H., Heat Exchangers: Selection, Rating and Thermal Design, CRC Press, 2002.

3. Bengtson, H., Fundamentals of Heat Exchangers, an online, continuing education course for PDH credit.

4. Bengtson, H., Thermal Design of a Double Pipe Heat Exchanger, and online blog article.

Natural Convection Heat Transfer Coefficient Calculator Spreadsheet

Posted on by
Reply

Where to Find a Natural Convection Heat Transfer Coefficient Calculator Spreadsheet

For an Excel spreadsheet to use as a natural convection heat transfer coefficient calculator, click here to visit our spreadsheet store.  Why search for heat transfer coefficient correlations or use online calculators, when you can buy a spreadsheet to use as a natural convection heat transfer coefficient calculator for five different configurations for only $14.95. Read on for information about natural convection heat transfer coefficients and Excel spreadsheets to obtain a value for them.

Convection heat transfer takes place between a solid surface and fluid that is at a different temperature and is in contact with the surface.  If the fluid is flowing past the surface due to an external driving force like a fan or pump, then the heat transfer is called forced convection.  When  fluid motion is due to density differences within the fluid (caused by temperature variation), then the heat transfer is called natural convection or free convection.

Newton’s Law of Cooling for Natural Convection Heat Transfer Coefficient Calculator

Newton’s Law of Cooling [ Q = hA(Ts – Tf) ] is a simple expression used for the rate of convective heat transfer with either forced or natural convection.  The parameters in Newton’s Law of Cooling are:

  • Q, the rate of forced convection heat transfer (Btu/hr – U.S. or W – S.I.)
  • Ts, the solid temperature (oF – U.S. or oC – S.I.)
  • Tf, the fluid temperature (oF – U.S. or oC – S.I.)
  • A, the area of the surface that is in contact with the fluid (ft2 – U.S. or m2 – S.I.)
  • h, the convective heat transfer coefficient (Btu/hr-ft2–oF – U.S. or W/m2-K – S.I.)

Dimensionless Nusselt, Rayleigh, Grashof, and Prandtl Numbers

natural convection heat transfer coefficient calculator dimensionless numbersA natural convection heat transfer coefficient calculator typically makes estimations using correlations of dimensionless numbers, specifically correlations of Nusselt number (Nu) with Prandtl number (Pr), Grashof number (Gr), and/or Rayleigh number (Ra), where Ra = GrPr.  The Nusselt, Grashof and Prandtl numbers are defined in the box at the left.

Following is a list of the parameters that appear in these dimensionless numbers, with units are given for both the U.S engineering system and S.I. system of units:

  • D, a characteristic length parameter (e.g. diameter for natural convection from a circular cylinder or a sphere or height of a vertical plate)  (ft for U.S.,  m for S.I.)
  • ρ, the density of the fluid  (slugs/ft3 for U.S.,  Kg/m3 for S.I.)
  • μ, the viscosity of the fluid  (lb-sec/ft2 for U.S.,  N-s/m2 for S.I.)
  • k, the thermal conductivity of the fluid  (Btu/hr-ft-oF for U.S.,  W/m-K for S.I.)
  • Cp, the heat capacity of the fluid  (Btu/lb-oF for U.S.,  J/kg-K for S.I.)
  • g, the acceleration due to gravity (32.17 ft/sec2 for U.S.,  9.81 m/s2 for S.I.)
  • β, the coefficient of volume expansion of the fluid  ( oR for U.S.,  K for S.I.)
  • ΔT, the temperature difference between the solid surface and the fluid  ( oF for U.S., oC or K for S.I.)

The following sections provide equations for estimating the heat transfer coefficient for several common natural convection configurations.

Natural Convection Heat Transfer Calculator for a Vertical Plane

natural convection heat transfer coefficient calculator correlationsThe box at the right shows two correlations for convection heat transfer between a vertical plane and a fluid of different temperature in contact with it.  The first can be used for all values of Rayleigh number and the second is only for laminar flow, indicated by Ra < 109.  The screenshot image below shows an example of an Excel spreadsheet to use as a natural convection heat transfer coefficient calculator for a vertical plate using the two equations shown here.

An Excel Spreadsheet as a Natural Convection Heat Transfer Calculator

For low cost, easy to use Excel spreadsheet packages to use as a natural convection heat transfer coefficient calculator for natural convection from a vertical plane, a horizontal plane, an inclined plane, a horizontal cylinder or a sphere in either U.S. or S.I. units (for only $16.95),  click here to visit our spreadsheet store.

Screenshot of a natural convection heat transfer coefficient calculator spreadsheet

References

1. Incropera, F.P., DeWitt, D.P, Bergman, T.L., & Lavine, A.S., Fundamentals of Heat and Mass Transfer, 6th Ed., Hoboken, NJ, John Wiley & Sons, (2007).

2. Lienhard, J.H, IV and Lienhard, J.H. V, A Heat Transfer Textbook: A Free Electronic Textbook

3. Bengtson, Harlan H, Fundamentals of Heat Transfer, an online continuing education course for engineering PDH credit

4. Bengtson, Harlan H., Convection Heat Transfer Coefficient Estimation, an online continuing education course for PDH credit.

Forced Convection Heat Transfer Coefficient Calculator

Posted on by

Where to Find a Forced Convection Heat Transfer Coefficient Calculator Spreadsheet

For an Excel spreadsheet to use as a forced convection heat transfer coefficient calculator, click here to visit our spreadsheet store.  Read on for information about forced convection heat transfer coefficients and their calculation.

An Excel spreadsheet can be a convenient forced convection heat transfer coefficient calculator.   This type of calculation is typically based on a correlation of dimensionless numbers, usually Nusselt number in terms of Reynolds number and Prandtl number.  Forced convection occurs with a fluid moving past a solid surface when the fluid and the solid are at different temperatures.  Newton’s Law of Cooling [ Q = hA(Ts – Tf) ] is a simple expression for the rate for convective heat transfer.  The parameters in Newton’s Law of Cooling are:

  • Q is the rate of forced convection heat transfer (Btu/hr – U.S. or W – S.I.)
  • Ts is the solid temperature (oF – U.S. or oC – S.I.)
  • Tf is the fluid temperature (oF – U.S. or oC – S.I.)
  • A is the area of the surface that is in contact with the fluid (ft2 – U.S. or m2 – S.I.)
  • h is the convective heat transfer coefficient (Btu/hr-ft2–oF – U.S. or W/m2-K – S.I.)

Dimensionless Numbers for a Forced Convection Heat Transfer Coefficient Calculator

Determining a good estimate for the heat transfer coefficient, h, is often the most difficult part of forced convection heat transfer calculations.  The process for estimating the heat transfer coefficient for a particular forced convection application is often through a correlation for Nusselt number (Nu) in terms of Reynolds number (Re) and Prandtl number (Pr).  These three dimensionless numbers are defined in the box below, along with the definitions of the parameters that appear in them.

Forced Convection Heat Transfer Coefficient Calculator Dimensionless Numbers

Nusselt Number Correlations for Turbulent Flow Inside a Pipe

The Dittus Boelter equation, which has been around since 1930 (ref #1) has two forms as follows:

Nuo = 0.023 Re0.8Pr0.4 , for ‘heating’ (temperature of wall > temperature of fluid), and

Nuo = 0.026 Re0.8Pr0.3 , for ‘cooling’ (temperature of wall < temperature of fluid).

Subject to: 0.7 < Pr < 120 ; 10,000 < Re < 160,000; L/D > 10 ( L/D > 50 according to some authors).  It is a rather simple equation to use, but has a fairly narrow range of acceptable values for Re and Pr.

Forced Convection Heat Transfer Coefficient Calculator Nusselt Number CorrelationsAnother correlation (from ref #2) is shown in the box at the right.  The range of values for Re and Pr for this correlation are also shown.  This correlation can be used for a wider range of values of Re and Pr.

A third correlation is shown in the box at the left below.  This correlation, described by Pethukov (ref #3) is only a minor variation of the second correlation shown at the right.  This third correlation works for an even wider range of values for Re and Pr.

Nusselt Number Correlation for Forced Convection Heat Transfer Coefficient CalculatorExcel spreadsheets can be conveniently used as a forced convection heat transfer coefficient calculator with correlations like these or others for configurations like laminar pipe flow, flow inside a circular annulus, flow outside a cylinder, flow past a bank of tubes, or flow in a noncircular cylinder, because the equations can be programmed into the spreadsheet using Excel formulas.  For free download of an Excel spreadsheet for calculating forced convection heat transfer coefficients for laminar pipe flow, and low cost spreadsheets for all of the other configurations mentioned above,  click here to visit our spreadsheet store.

References

1.  Dittus, P.W. and Boelter, L.M., Univ. Calif. Pub. Eng., Vol. 1, No. 13, pp 443-461 (reprinted in Int. Comm. Heat Mass Transfer, Vol. 12, pp 3-22 (1985).

2.  egr.msu.edu

3.  Petukhov, B.S., “Heat transfer and friction in turbulent pipe flow with variable physical properties,” Adv. Heat Transfer 6, 503-565 (1970).