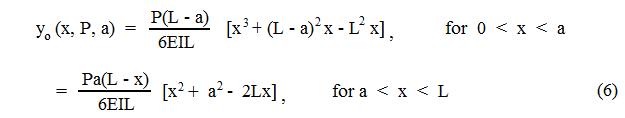Where to Find a Time Value of Money Excel Spreadsheet
To obtain a time value of money Excel spreadsheet, click here to visit our spreadsheet store. Read on for information about the use of a time value of money Excel spreadsheet.
Time value of money formulas—present worth, future worth, equivalent cash flow, and so on—are essential tools for engineering and financial analysts concerned with calculating the costs and benefits of multi-year investments. The formulas provide analysts with a consistent way to evaluate various alternative financial scenarios. For example, in trying to decide between buying an expensive production machine with low annual maintenance costs or a cheaper machine with high annual maintenance costs, the analyst could convert the series of annual maintenance costs to equivalent lump sums of cash held at the present time. Adding these sums to the initial costs of the respective machines would then give a consistent measure of the total cost of buying one machine compared with the other.
Explicit formulas for time value of money calculations including converting a series of future costs to a lump sum will now be given.
Time Value of Money Excel Spreadsheet Formulas
The concept of time value of money refers to the fact that a sum of money is more valuable to you if you possess it right now compared to possessing it at some time in the future. The difference in value arises from the interest that you can earn on the money, if you possess it now. For example, suppose that a sum of money, P, that you possess now, can be invested for a year at an interest rate, i. At the end of the year, you have earned an amount of interest of i times P, so that you now have the following amount:
Amount after one year = P + iP
= P(1 + i)
In the second year, you start out with an amount P(1 + i). The interest you earn on this amount is then, i times P(1 + i), so that at the end of the second year you have a larger amount:
Amount after two years = P(1 + i) + iP(1 + i)
= P(1 + i)2
Continuing in this fashion for n years, you have a sum, F, given by
F = P(1 + i)n ……………………………………………………(1)
F is called the “future worth”; P is called the “present worth.”
The convention in the field of time value of money is to use the following notation to denote the factor (1 + i)n:
(F|P i,n) = (1 + i)n …………………………………………..(2)
The quantity (F|P i,n) is called the “single sum, future worth factor.” Eq. 1 can now be written as
F = P (F|P i,n)…………………………………………………(3)
Solving Eq. 1 for P produces a formula for the present worth, given the future worth:
P = F (P|F i,n)………………………………………………..(4)
where
(P|F i,n) = (1 + i)-n
The quantity (P|F i,n) is called the “single sum, present worth factor.”
Similar calculations lead to formulas that relate present worth and future worth to the magnitude, A, of a uniform cash flow (receipt or disbursement) at the end of each time period. For example, A is related to the future worth F through the “sinking fund factor” (A|F i,n):
A = F (A|F i,n)…………………………………………………….(5)
= F { i/[(1 + i)n – 1] }
The magnitude A of the cash flow is related to the future worth through the “capital recovery factor” (A|P i,n):
A = P (A|P i,n)……………………………………………………(6)
= P { i(1 + i)n/[(1 + i)n – 1] }
Inverting Eqs. 5 and 6 gives the future worth and present worth equivalent to the magnitude A.
F = A (F|A i,n)…………………………………………………..(7)
= A { [(1 + i)n – 1]/i }
where (F|A i,n) is the uniform series, future worth factor, and
P = A (P|A i,n)…………………………………………………..(8)
= A { [(1 + i)n – 1]/i(1 + i)n }
where (P|A i,n) is the uniform series, present worth factor.
Analogous formulas can be written for the non-uniform series cases of gradient series of cash flows (cash flows in which each cash flow amount increases by a fixed amount over the previous cash flow) and a geometric series of cash flows (cash flows in which each cash flow amount increases by a fixed percent from one time period to the next).
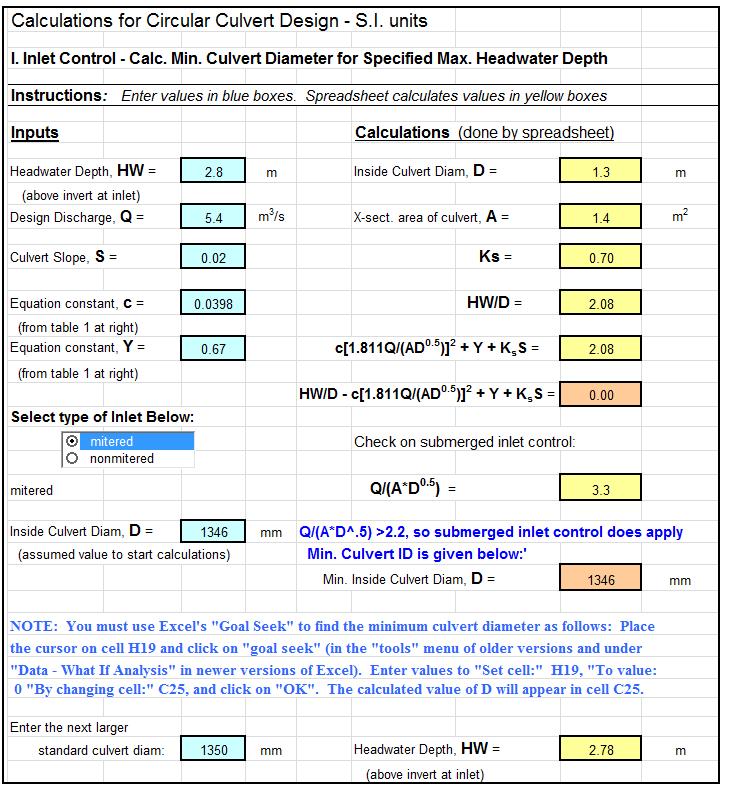
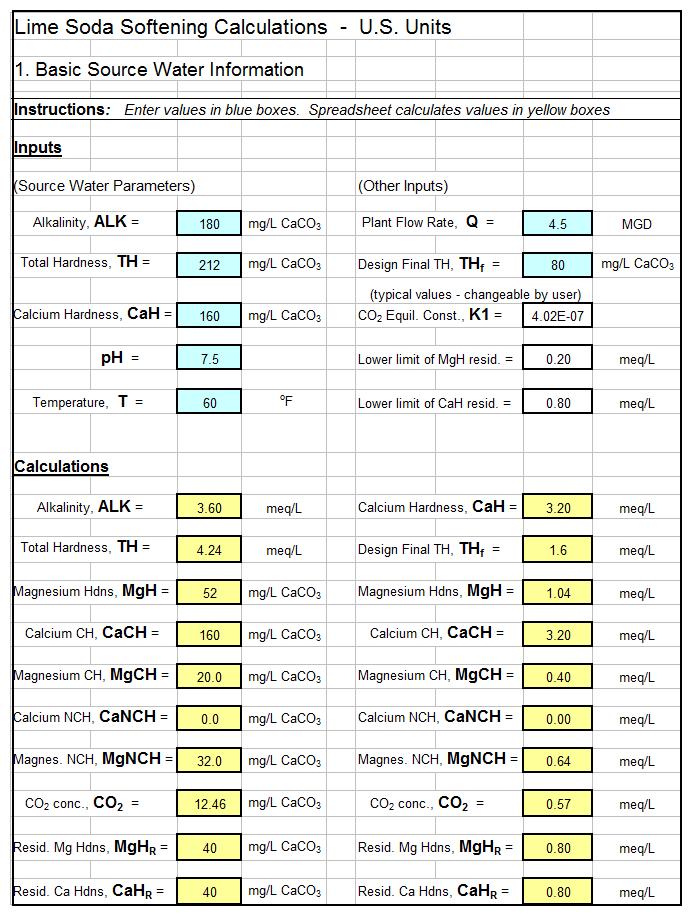
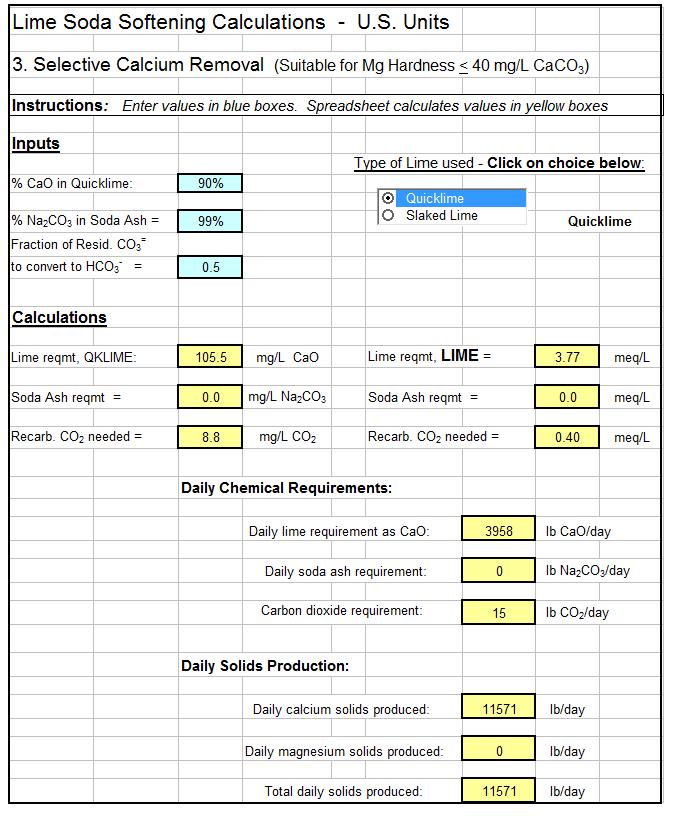
Screenshot of a Time Value of Money Excel Spreadsheet
Eqs. 3-8 are used so frequently in financial calculations that Excel provides three built-in functions—PV( ), FV( ), and PMT( )—that will compute P, F, or A, depending on what arguments are used as inputs. These formulas are compact and easy to type into a worksheet cell, but they have the drawbacks that you must remember or look up 1) the name of the function, 2) the purpose of the function, and 3) the order and definition of the arguments. All these drawbacks would be eliminated with proper spreadsheet design, specifically, if labels are provided next to the input and output cells—thus the spreadsheet user never even sees PV( ), FV( ), and PMT( ). A further convenience would be, when you need to calculate a pair of values (for example, P and F, or F and A), based on common input such as i and n, that you would enter i and n only once. This arrangement is shown in the screenshot image of the workbook shown in Figure 1. The user enters the common data, n and i, only once. Then all formulas for P, F, and A can be evaluated by entering a single additional number into an appropriately labeled cell. Input is thus reduced to an absolute minimum, and the probability of making an error is correspondingly reduced.
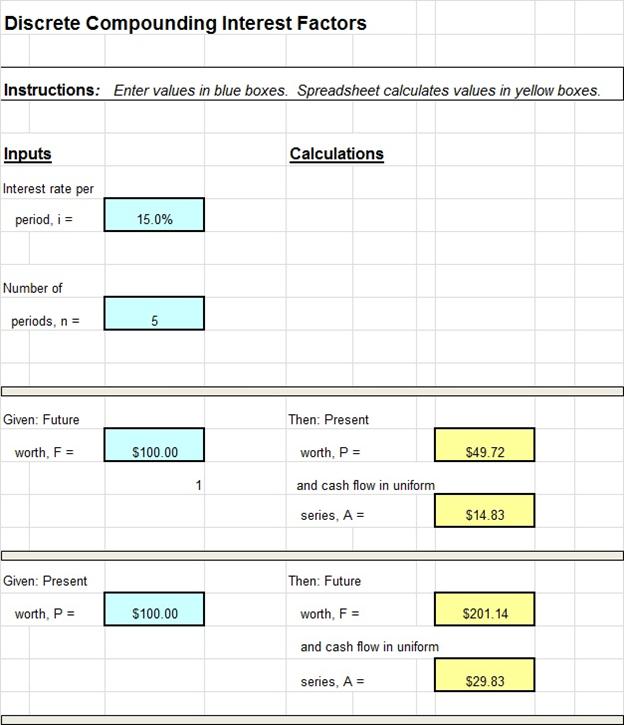
Figure 1. Screenshot showing calculation of P and A, given F, and of F and A, given P
Continuous Compounding for Discrete Flows
The above discussion was concerned with time value calculations corresponding to interest payments made at the end of a time period, that is, discrete compounding. If the time periods become shorter and more frequent, then the limiting case (in the sense of calculus) of continuous compounding is obtained. It can be shown that the time value of money formulas now involve e, the base of the natural logarithms, as shown below.
Discrete flow, continuous compounding, single sum present worth factor:
P = F (P|F r,n)∞
= Fe-rn
Discrete flow, continuous compounding, sinking fund factor:
A = F (A|F r,n)∞
= F (er -1)/(ern – 1)
Discrete flow, continuous compounding, single sum future worth factor:
F = P (F|P r,n)∞
= Pern
Discrete flow, continuous compounding, capital recovery factor:
A = P (A|P r,n)∞
= P [ ern (er -1)/(ern – 1) ]
Discrete flow, continuous compounding, uniform series present worth factor:
P = A (P|A r,n)∞
= A [ (ern -1)/ ern (er – 1) ]
Discrete flow, continuous compounding, uniform series future worth factor:
F = A (F|A r,n)∞
= A [ (ern -1)/(er – 1) ]
Excel does not contain special functions for continuous compounding of discrete flows, so you must program them yourself by using the exponential function Exp( ). Thus the availability of a specialized workbook similar to that shown in Figure 1 is even more useful here than in the discrete compounding case.
Continuous Compounding for Continuous Flows
All the above formulas are based on the assumption that cash flows occur at discrete increments at the end of time periods such as months or days. If, instead, we assume that a total A of money flows continuously and uniformly throughout a given time period, then the result is referred to as “continuous flow.” It can be shown that the following formulas apply in this case.
Continuous flow, continuous compounding uniform series present worth factor:
P = A (P|A r,n)
= A [(ern – 1)/rern ]
Continuous flow, continuous compounding uniform series future worth factor:
F = A (F|A r,n)
= A [(ern – 1)/r ]
Continuous flow, continuous compounding capital recovery factor:
A = P (A|P r,n)
= P[ rern /(ern – 1) ]
Continuous flow, continuous compounding sinking fund factor:
A = F (A|F r,n)
= F [ r / (ern – 1) ]
As was the case for continuous compounding of discrete flows, Excel does not contain special functions for continuous compounding of continuous flows, and so you must program them yourself by using the exponential function Exp( ). Again the availability of a specialized workbook similar to that shown in Figure 1 is quite useful for applying these formulas.
The workbook of which the spreadsheet of Figure 1 is a part contains tabs for discrete compounding, continuous compounding for discrete flows and continuous compounding for continuous flows. Because all formulas used in each tab are visible and can be unlocked, users possessing only a basic knowledge of Excel may easily customize the spreadsheet to meet particular needs and recurring applications. This Excel workbook is available at low cost in our spreadsheet store.
References
1. Riggs, J.L., Bedworth, D.D., and Randhawa, S.U., Engineering Economics, 4th ed., McGraw-Hill, New York, NY (1987).
2. White, J.A., Agee, M.H., and Case, K.E., Principles of Engineering Economic Analysis, 3rd ed., Wiley, New York, NY (1989).
3. Megginson, W.L., Smart, S.B., and Lucey, B.M., Introduction to Corporate Finance, Cengage Learning, London (2008).
4. Brigham, E.F., and Ehrhardt, M.C., Financial Management, Thomson South-Western, Mason, OH (2008).
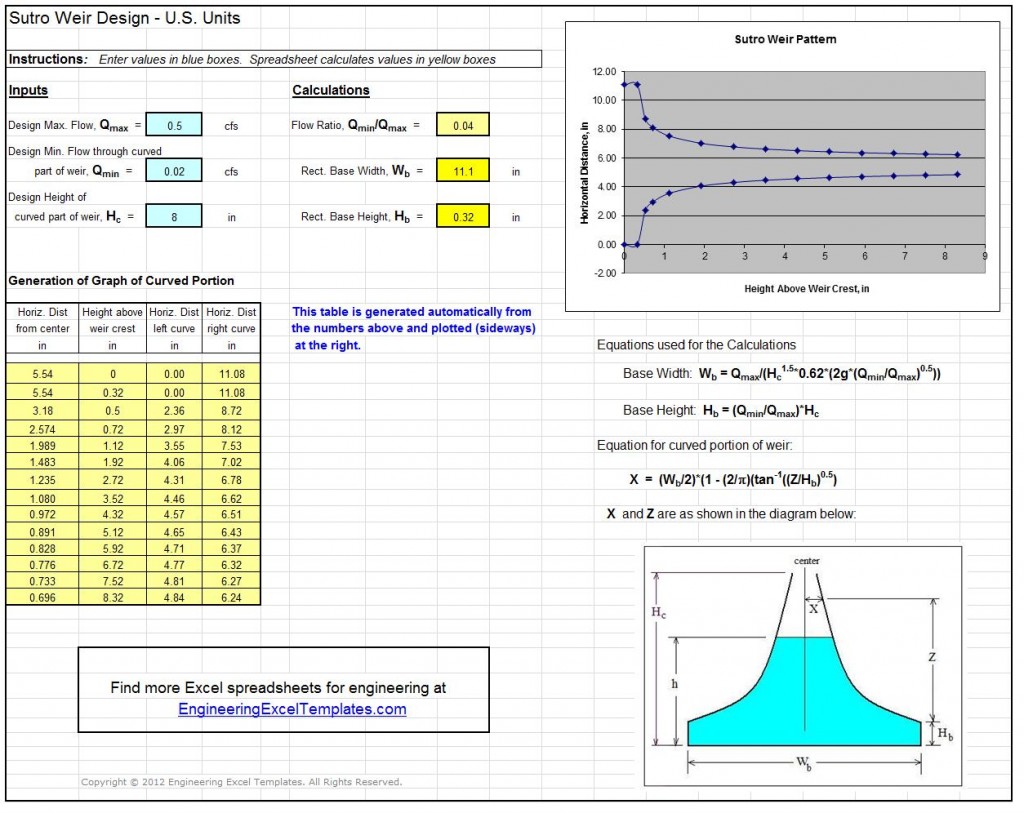
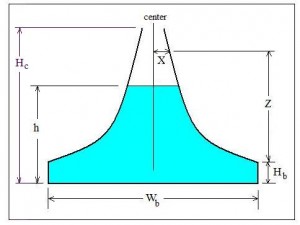 increases as the head over the weir increases, but the flow rate increases at a faster rate than the head over the weir. For some applications, it is desirable for the flow rate over a weir to be proportional to the head over the weir. The sutro weir, also known as a proportional weir accomplishes this by having the width of the opening above the weir crest decrease with increasing head over the weir crest as shown in the diagram of a sutro weir at the right. Equations that can be used for proportional sutro weir design are discussed in the next section.
increases as the head over the weir increases, but the flow rate increases at a faster rate than the head over the weir. For some applications, it is desirable for the flow rate over a weir to be proportional to the head over the weir. The sutro weir, also known as a proportional weir accomplishes this by having the width of the opening above the weir crest decrease with increasing head over the weir crest as shown in the diagram of a sutro weir at the right. Equations that can be used for proportional sutro weir design are discussed in the next section.