Where to get a Proportional Sutro Weir Design Calculation Excel Spreadsheet
For a proportional sutro weir design calculation Excel spreadsheet in either U.S. or S.I. units, click here to visit our spreadsheet store. Obtain convenient, easy to use spreadsheets for proportional sutro weir design calculations at reasonable prices. Read on for information about the use of a proportional sutro weir design calculation Excel spreadsheet.
Principles of a Proportional Sutro Weir Design Calculation Excel Spreadsheet
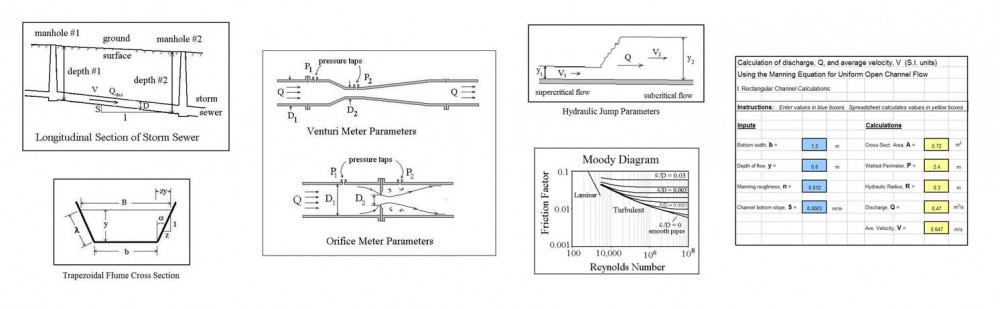
For the commonly used rectangular weir or V-notch weir, the flow rate over the weir 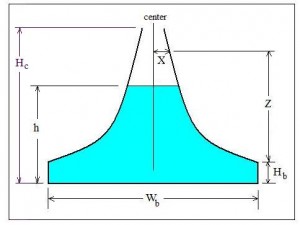 increases as the head over the weir increases, but the flow rate increases at a faster rate than the head over the weir. For some applications, it is desirable for the flow rate over a weir to be proportional to the head over the weir. The sutro weir, also known as a proportional weir accomplishes this by having the width of the opening above the weir crest decrease with increasing head over the weir crest as shown in the diagram of a sutro weir at the right. Equations that can be used for proportional sutro weir design are discussed in the next section.
increases as the head over the weir increases, but the flow rate increases at a faster rate than the head over the weir. For some applications, it is desirable for the flow rate over a weir to be proportional to the head over the weir. The sutro weir, also known as a proportional weir accomplishes this by having the width of the opening above the weir crest decrease with increasing head over the weir crest as shown in the diagram of a sutro weir at the right. Equations that can be used for proportional sutro weir design are discussed in the next section.
Equations for Proportional Sutro Weir Design Calculation Excel Spreadsheet
Equations for the base width and base height of a sutro weir are as follows:
- Wb = base width in ft (m for S.I. units)
- Hb = base height in ft (m for S.I. units)
- Hc = max height or curved portion of weir in ft (m for S.I. units)
- Qmax = design maximum flow over the weir in cfs (m3/s for S.I. units)
- Qmin = design minimum flow over the weir in cfs (m3/s for S.I. units)
- g = acceleration of gravity = 32.17 ft/s/s (9.81 m/s/s for S.I. units)
The equation for the curved portion of a proportional sutro weir is:
X and Z are position parameters as shown in the diagram above. They will have the same units as Wb .
A Screenshot for a Proportional Sutro Weir Design Calculation Excel Spreadsheet
For a proportional sutro weir design calculation Excel spreadsheet with calculations in S.I. or U.S. units, or for other spreadsheets for open channel flow measurement calculations, see: www.engineeringexceltemplates.com
The Excel spreadsheet screenshot below shows part of a spreadsheet for proportional sutro weir design calculations, available at our spreadsheet store in either U.S. or S.I. units at a very reasonable price.
Reference
1, U.S. DOT, Fed Highway Admin, Urban Design Manual, Circular No. 22, 2nd Ed. 2001 (Publ. No. FHWA-NHI-010021-HEC-22)
2. Bengtson, Harlan H., “Proportional Weir Design Equations,” an online blog article