Where to Find a Horizontal Flow Grit Chamber Spreadsheet
To obtain a spreadsheet for Horizontal Flow Grit Chamber Design, click here to visit our spreadsheet store. This Excel spreadsheet has worksheets for calculating the peaking factor and for calculating the required dimensions for the horizontal flow grit chamber based on user input values for several parameters . There is also a worksheet for design of the exit sutro weir to control the horizontal velocity in the grit chamber. You can buy a convenient horizontal flow grit chamber spreadsheet for a very reasonable price. It is available in either U.S. units or S.I. units. Read on for background information about a Horizontal Flow Grit Chamber Design spreadsheet.
Background for a Horizontal Flow Grit Chamber Design Spreadsheet
The size and dimensions of a horizontal flow grit chamber are typically based on the detention time and horizontal velocity. Table 1, shown below, gives typical values for the design parameters, detention time and horizontal velocity, as well as typical added length for .the inlet and outlet.
Table 1. Typical Values for Design Parameters for Horizontal flow Grit Chamber
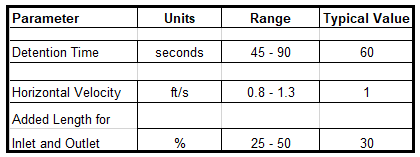
Exit Sutro Weir Design
A sutro weir is typically used as the exit from a horizontal flow grit chamber, because it maintains a constant horizontal velocity through the grit chamber. The diagram below shows the shape of a sutro weir, as plotted for an example horizontal flow grit chamber.
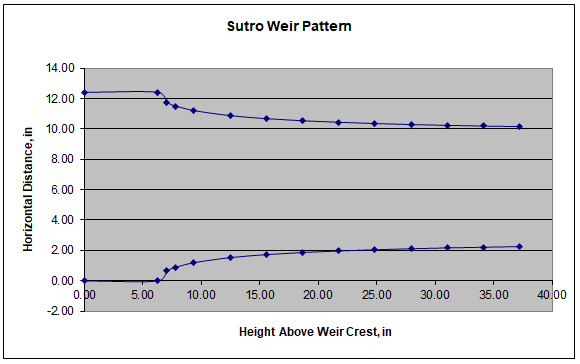
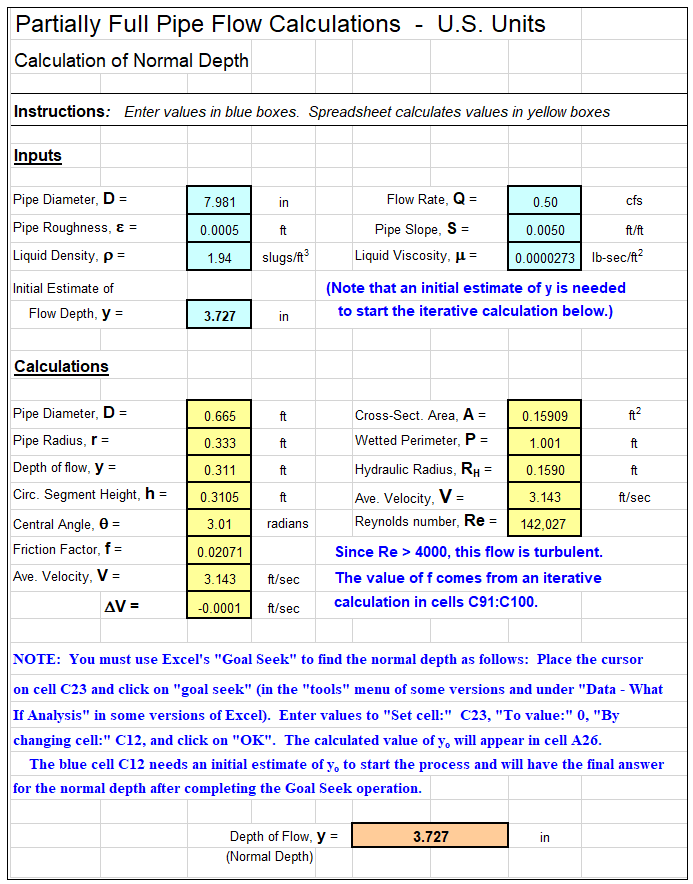
Example Horizontal Flow Grit Chamber Spreadsheet
An example Horizontal Flow Grit Chamber Design spreadsheet is partially shown in the image below. . This Excel spreadsheet can be used to calculate the required tank volume, tank length and tank depth, .based on user input values for wastewater flow rate, design horizontal velocity, detention time, and tank width.. This Excel spreadsheet, as well as others for water and wastewater treatment calculations, is available in either U.S. or S.I. units for a very reasonable price in our spreadsheet store.n
References:
1. Metcalf & Eddy, Inc, (Revised by Tchobanoglous, G, Burton, F.L, Stensel, H.D.), Wastewater Engineering, Treatment and Resource Recovery, 5th Ed., New York, NY, 2014.
2. Bengtson, Harlan H., “Horizontal Flow Grit Chamber Design Calculations,” an online blog article.